预科数学
第一部分:实数运算
第一节:自然数
- 该分支下无内容
第二节:分数与小数
- 该分支下无内容
第三节:比例式
- 比例式的性质
- 中间项的乘积等于两边项的乘积
- 交换中间项仍成立
- 交换两边项仍成立
- 分别交换等式两边的分子分母仍成立
- 交换等式两边的比例式仍成立
- Если $\frac{а}{b}=\frac{c}{d}$
- $\frac{а}{c}=\frac{b}{d}$
- $\frac{d}{b}=\frac{c}{a}$
- $\frac{b}{a}=\frac{d}{c}$
- $\frac{c}{d}=\frac{a}{b}$
- $\frac{b}{d}=\frac{a}{c}$
- $\frac{c}{a}=\frac{d}{b}$
- $\frac{d}{c}=\frac{b}{a}$
第四节:数集
- 该分支下无内容
第五节:有理数运算
- 运算优先级
- 平方、开方
- 乘方、除法
- 加法、减法
第六节:低次方程
- 韦达定理
- 原式:$ax^2+bx+c=0$
- 二次项系数化一:$x^2+px+q=0$
- 求根公式:$x_{1,2}=\frac{-p}{2}\pm\sqrt{\left(\frac{p^2}{4-q}\right)}$
- 韦达定理:
- $x_1+x_2=-p$
- $x_1x_2=q$
第七节:一次不等式与绝对值不等式
- 一次不等式
- 基本形式 $\left(a\neq0\right)$
- $ax+b>0$
- $ax+b<0$
- $ax+b\geq0$
- $ax+b\le0$
- 性质:不等式两边同乘负数时不等式的符号颠倒(при умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный)
第八节:代数方程组
- 该分支下无内容
第九节:代数不等式
- 不等式
- 严格不等式 строгое неравенство
- $f\left(x\right)>g\left(x\right)$
- 不严格不等式 нестрогое неравенство
- $f\left(x\right)\geq g\left(x\right)$
- 性质1:
- 加减同一个表达式后的等式与原等式等价
- $f\left(x\right)\pm p\left(x\right)>g\left(x\right)\pm p\left(x\right)$ 等价于 $f\left(x\right)>g\left(x\right)$
- 性质2:$f\left(x\right)>g\left(x\right)$
- 乘以一个大于0的数不等式符号方向不变
- $af\left(x\right)>ag\left(x\right) \quad (а>0)$
- 乘以一个小于0的数不等式符号方向改变
- $af\left(x\right)<ag\left(x\right) \quad (a<0)$
- 乘以一个大于0的数不等式符号方向不变
- 复杂的不等式
- $\frac{f\left(x\right)}{g\left(x\right)}>0$
- $\frac{f\left(x\right)}{g\left(x\right)}\geq0$
- $\frac{f\left(x\right)}{g\left(x\right)}<0$
- $\frac{f\left(x\right)}{g\left(x\right)}\le0$
- 二次不等式 квадратное неравенство
- 间隔法 метод интервалов
- 或许是国内的穿根法?
- 详情
- 严格不等式 строгое неравенство
第十节:无理方程
- 解无理数方程一般方法:
- 确定定义域(ОДЗ,Область Допуспимых Значений,允许值范围)
- 将等式两边提升至需要的幂
- 提升至偶数幂之后可能会导致定义域扩大和增根出现
- 将最后得到的根带入原方程检验
第十一节:无理不等式
- $\sqrt{f\left(x\right)}<\phi\left(x\right)$ 型无理不等式解法
- 满足以下条件有解:
- $f\left(x\right)\geq0$
- $\phi\left(x\right)>0$
- $f\left(x\right)<\phi^2\left(x\right)$
- 满足以下条件有解:
- $\sqrt{f\left(x\right)}>\phi\left(x\right)$ 型无理不等式解法
- $\phi\left(x\right)>0$时,满足以下条件有解:
- $f\left(x\right)\geq0$
- $\phi\left(x\right)<0$
- $\phi\left(x\right)\geq0$ 时,满足以下条件有解:
- $\phi\left(x\right)\geq0$
- $f\left(x\right)\geq0$
- $f\left(x\right)>\phi^2\left(x\right)$
- 不等式的解是以上两种情况的子集
- $\phi\left(x\right)>0$时,满足以下条件有解:
- $\sqrt{f\left(x\right)}\le\phi\left(x\right)$ 型无理不等式解法
- 满足以下条件有解:
- $f\left(x\right)\geq0$
- $\phi\left(x\right)\geq0$
- $f\left(x\right)\le\phi^2\left(x\right)$
- 满足以下条件有解:
- $\sqrt{f\left(x\right)}\geq\phi\left(x\right)$ 型无理不等式解法
- $\phi\left(x\right)<0$ 时,满足以下条件有解:
- $f\left(x\right)\geq0$
- $\phi\left(x\right)\le0$
- $\phi\left(x\right)\geq0$ 时,满足以下条件有解:
- $\phi\left(x\right)\geq0$
- $f\left(x\right)\geq0$
- $f\left(x\right)\geq\phi^2\left(x\right)$
- 不等式的解是以上两种情况的子集
- $\phi\left(x\right)<0$ 时,满足以下条件有解:
第二部分:基本初等函数
第一节:一次函数与二次函数的图像
- 一次函数
- 形式:$y=ax+b \quad R \to R$
- 模式:$y=ax+b \quad 定义域 \to 值域$
- 二次函数
- 一般式:$y=ax^2+bx+c \quad R \to R$
- 顶点式 $y=a\left(x-h\right)^2+k$
- $h=\frac{b}{2a}$
- $k=\frac{\left(4ac-b^2\right)}{4a}$
- 最值:$k$
- 对称轴:$h$
- 韦达定理:$x_1-x_2=-\frac{b}{a}$
- 求根公式:$x_{1,2}=\frac{-b\pm\sqrt{\Delta}}{2a}$
第三部分:指数与对数
第一节:指数函数与对数函数
- 指数函数
- 定义:形如 $y=a^x (a>0,a≠1)$ 的函数叫做指数函数
- 指数函数的定义域是整个实数集
- 指数函数的值域是正数集
- 指数函数中,对于任意的 $x$ 的值,都有 $y>0$,所以指数函数的图像不穿过 $x$ 轴
- 指数函数既不是偶函数也不是奇函数
- $a>1$ 时,函数为增函数;$0<a<1$ 时,函数为减函数
- 指数函数的图象是一条穿过点 $(0;1)$ 的曲线
- 对数及其性质
- 指数 $c$ 叫做以 $a(a>0,a≠1)$ 为底正数 $b$ 的对数,需将 $a$ 升到 $c$ 次幂,才能得到数字 $b$:$a^c=b$,$c=\log_a{b}$
- $\log_a{b}$ 读作:логарифм числа b по основанию a
- 正数 $b$ 的十进制对数(десятичный логарифм,国内又叫常用对数)是以十为底的 $b$ 的对数,写作:$\log{b}$
- 正数 $b$ 的自然对数(натуральный логарифм)是以 $e$ 为底的 $b$ 的对数,写作:$\ln{b}$
- 其中 $b$ 是无理数,$b=2,71828…$
- 当 $a>0,a≠1,b>0,c>0$ 时,对数具有以下性质:
- $\log_a{a}=1$
- $\log_a{1}=0$
- $\log_a{\left(bc\right)}=\log_a{b}+\log_b{c}$
- $\log_a{b/c}=\log_a{b}-\log_a{c}$
- $\log_a{b^p}=p\log_a{b}$
- $\log_a{p^b}=\frac{1}{p}\log_a{b}$,p≠1
- $a^{\log_b{c}}=c^{\log_b(a)}$
- $\log_a{b}=\frac{\log_c{b}}{\log_c(a)} \quad (c≠1)$ (换底公式)
- $\log_a{b}=\frac{1}{\log_ba} \quad(a>0,a≠1,b>0,b≠1)$
- $\log_a{b}=\log_{a^p}{b^p}$
- 根据给出的底数找出数的对数的运算称为找出对数(логарифмирование)
- 根据给出的底数找出对数的真数的运算称为对数还原(потенцирование)
- 对数函数
- 定义:形如 $y=log_a{x} \quad (a>0,a≠0)$ 的函数叫做对数函数
- 对数函数的定义域是整个正数集
- 对数函数的值域是实数集
- 对数函数的图象穿过 $x$ 轴上的点 $(1;0)$
- 对数函数既不是偶函数也不是奇函数
- $a>1$ 时,对数函数单调递增;$0<a<1$ 时,对数函数单调递减
- $a>1$ 时
- $log_a{x}>0 \quad (x>1)$
- $log_a{x}<0 \quad (0<x<1)$
- $0<a<1$ 时
- $log_a{x}>0 \quad (0<x<1)$
- $log_a{x}<0 \quad (x>1)$
- $a>1$ 时
- 对数函数的图象是一条穿过点 $(1;0)$ 的曲线
- 因为对数函数与指数函数互为反函数,所以函数 $y=log{x}$ 与 $y=a^x$ 的图像关于直线 $y=x$ 对称
第二节:对数表达式
- 该分支下无内容
第三节:指数幂方程
- 形式:$a^{f\left(x\right)}=t \quad (t>0)$
第四节:不等指数方程
- 解法
- 使方程左右两边底数相同
- 在 1 的基础上换元
- 在 2 的基础上移项式方程一边为 0,后除以一个带指数 $x$ 的项
- 分类讨论
第五节:对数方程
- 在对数符号或对数底中包含变量的方程称为对数方程
- 在求解对数方程时,一定要考虑定义域和对数的性质。
- 如果要找到未知数的定义域是一项困难的任务,将求得的根代入原方程进行检验,以消除外来根。
- 解决同时具有指数和对数特征的方程的方法是对这两部分进行对数化的方法
第六节:对数不等式(组)
- 解法
- 写出满足题目所给不等式(组)的函数的定义域
- 运用化同底和换元法求出函数的另一组定义域
- 将两组定义域取交集
- 注意事项
- 一定要注意对数方程的定义域(底数>0且≠1,真数>0)
- 熟练运用对数的性质将不等式方程左右两边化为同底的对数
- 当方程中有较为繁琐的对数方程时可以考虑用换元法简化方程
- 在对数不等式(组)中如果出现绝对值,其中的一部分可以通过写出方程自带的定义域后直接化简
- 较为常用的公式
- $\log_a{1}=0$
- $\log_a{\left(bc\right)}=\log_a{b}+\log_b{c}$
- $\log_a{\frac{b}{c}}=\log_a{b}-\log_a{c}$
- $\log_a{b}=\frac{\log_c{b}}{\log_c{a}} \quad(c≠1)$
- $\log_a{b}=\frac{1}{\log_ba}\quad (a>0,a≠1,b>0,b≠1)$
- 对于 $log_a{f\left(x\right)}>log_a{g\left(x\right)}$
- 当 $a>1$ 时
- $f\left(x\right)>g\left(x\right)$
- $f\left(x\right)>0$
- $g\left(x\right)>0$
- 当 $0<a<1$ 时
- $f\left(x\right)<g\left(x\right)$
- $f\left(x\right)>0$
- $g\left(x\right)>0$
- 当 $a>1$ 时
- 对于 $\log_{f\left(x\right)}\phi_1\left(x\right)>\log_{f\left(x\right)}\phi_2\left(x\right)$
- 当 $f\left(x\right)>1$ 时
- $\phi_1\left(x\right)>\phi_2\left(x\right)$
- $\phi_2\left(x\right)>0$
- 当 $0<f\left(x\right)<1$ 时
- $\phi_1\left(x\right)<\phi_2\left(x\right)$
- $\phi_1\left(x\right)>0$
- 当 $f\left(x\right)>1$ 时
第四部分:三角函数
第一节:角
- 弧度:弧度是角的度量单位。它是由国际单位制导出的单位,单位缩写是rad(рад)。定义:弧长等于半径的弧,其所对的圆心角为1弧度。(即两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时,两条射线的夹角的弧度为1)。
- 弧度与角度的转化遵循以下公式:
$$1рад=\frac{180^\circ}{\pi}\approx 57^\circ 17^\prime 45^{\prime \prime}$$ $$1^\circ = \frac{\pi}{180^\circ} \approx 0.01745рад$$ $$l=\frac{\pi r n}{180^\circ}=r\alpha$$
其中n为圆心角的大小(角度),r为半径
- 三角函数
- 正弦函数(Синус):在直角三角形中,将大小为 $\alpha$(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值 $\sin\alpha$,在平面直角坐标系中,正弦函数的值域在第一和第二象限为正,在第三和第四象限为负
- 余弦函数(Косинус):在直角三角形中,将大小为 $\alpha$(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值 $\cos\alpha$,在平面直角坐标系中,余弦函数的值域在第一和第四象限为正,在第二和第三象限为负
- 正切函数(Тангенс):在直角三角形中,将大小为 $\alpha$(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值 $\tan\alpha$在平面直角坐标系中,正切函数的值域在第一和第三象限为正,在第二和第四象限为负
- 余切函数(Котангенс):在直角三角形中,将大小为 $\alpha$(单位为弧度)的角邻边长度比对边长度的比值求出,函数值为上述比的比值 $\cot\alpha$ 在平面直角坐标系中,余切函数的值域在第一和第三象限为正,在第二和第四象限为负
第二节:三角简化公式(三角函数诱导公式)
- 三角函数简化公式可将任意角度的三角函数变为锐角的三角函数,即 $\alpha\in(0,\frac{\pi}{2})$
- 具体如下:
- 对于角 $(2\pi\pm\alpha)$ 和 $(\pi\pm\alpha)$,保留函数类型
- 对于角 $(\frac{\pi}{2}\pm\alpha)$ 和 $(\frac{3\pi}{2}\pm\alpha)$,替换给定函数的类型为其对应的函数类型(余函数),即正弦被余弦取代,正切被余切取代,反之亦然。
- 若角被认为是锐角,则得到的简化函数被赋予其原函数在第四象限的符号。
总结:奇变偶不变;符号看象限
- 简化公式表: | 函数 | | | | 角度$\phi$ | | | | |------|-----|-----|-----|-----|-------|-----|------| | 函数 | $\frac{\pi}{2}-\alpha$ | $\frac{\pi}{2}+\alpha$ | $\pi-\alpha$ | $\pi+\alpha$ | $\frac{3\pi}{2}-\alpha$ | $\frac{3\pi}{2}+\alpha$ | $2\pi-\alpha$ | | $\sin{\phi}$ | $\cos{\alpha}$ | $\cos{\alpha}$ | $\sin{\alpha}$ | $-\sin{\alpha}$ | $- \cos{\alpha}$ | $- \cos{\alpha}$ | $-\sin{\alpha}$ | | $\cos{\phi}$ | $\sin{\alpha}$ | $-\sin{\alpha}$ | $- \cos{\alpha}$ | $- \cos{\alpha}$ | $-\sin{\alpha}$ | $\sin{\alpha}$ | $\cos{\alpha}$ | | $\tg{\phi}$ | $\ctg{\alpha}$ | $-\ctg{\alpha}$ | $-\tg{\alpha}$ | $\tg{\alpha}$ | $\ctg{\alpha}$ | $-\tg{\alpha}$ | $-\tan{\alpha}$ | | $\tg{\phi}$ | $\tg{\alpha}$ | $-\tg{\alpha}$ | $-\ctg{\alpha}$ | $\cot{\alpha}$ | $\tg{\alpha}$ | $-\tg{\alpha}$ | $-\ctg{\alpha}$ |
第三节:三角函数公式
- 基本公式:
- $\sin^2\alpha+ \cos^2\alpha=1$
- $\tg\alpha=\frac{\sin\alpha}{ \cos\alpha}$,且 $\alpha\neq\frac{2k+1}{2}\pi,k\in Z$
- $\ctg\alpha=\frac{1}{tg\alpha}=\frac{ \cos\alpha}{\sin\alpha}$,且 $\alpha\neq k\pi,k\in Z$
- $1+\tg^2\alpha=\frac{1}{ \cos^2\alpha}$,且 $\alpha\neq\frac{\pi}{2}(2n+1),n\in Z$
- $1+\ctg^2\alpha=\frac{1}{\sin^2\alpha}$,且 $\alpha\neq\pi n,n\in Z$
-
用其他函数的值表示的某些三角函数的值: $$ \begin{aligned} &\sin\alpha=\pm\sqrt{1- \cos^2\alpha}=\frac{\tg\alpha}{\pm\sqrt(1+\tg^2\alpha)}=\frac{1}{\pm\sqrt{1+\ctg^2\alpha}}\ &\cos\alpha=\pm\sqrt{1-\sin^2\alpha}=\frac{1}{\pm\sqrt(1+\tg^2\alpha)}=\frac{\ctg\alpha}{\pm\sqrt(1+\ctg^2\alpha}\ &\tg\alpha=\frac{\sin\alpha}{\pm\sqrt(1-\sin^2\alpha)}=\frac{\pm\sqrt(1- \cos^2\alpha)}{ \cos\alpha}=\frac{1}{\ctg\alpha}\ &\ctg\alpha=\frac{\pm\sqrt(1-\sin^2\alpha)}{sin\alpha}=\frac{ \cos\alpha}{\pm\sqrt(1+ \cos^2\alpha)}=\frac{1}{\tg\alpha} \end{aligned} $$
-
三角函数的加、减和转换公式: $$ \begin{aligned} \sin{(\alpha\pm\beta)}&=\sin{\alpha} \cos{\beta}\pm \cos{\alpha}\sin{\beta}\ \cos{(\alpha\pm\beta)}&= \cos{\alpha} \cos{\beta}\mp \sin{\alpha}\sin{\beta}\ \tg{(\alpha\pm\beta)}&=\frac{\tg{\alpha}\pm \tg{\beta}} {1\mp \tg{\alpha}\tg{\beta}}\ \ctg{(\alpha\pm\beta)}&=\frac{\ctg{\alpha}\ctg{\beta}\mp1} {\ctg{\alpha}\pm \ctg{\beta}} \end{aligned} $$
-
倍角公式: $$ \begin{aligned} \sin2\alpha&=2\sin\alpha \cos\alpha\ \sin3\alpha&=3\sin\alpha-4\sin^3\alpha\ \cos2\alpha&=\cos^2\alpha-\sin^2\alpha\ \cos3\alpha&=4\cos^3\alpha-3 \cos\alpha\ \tg2\alpha&=\frac{2\tg\alpha}{1-\tg^2\alpha}\ \tg3\alpha&=\frac{3\tg\alpha-\tg^3\alpha}{1-3\tg^2\alpha}\ \ctg2\alpha&=\frac{\ctg^2\alpha-1}{2\ctg\alpha}\ \ctg3\alpha&=\frac{\ctg^3\alpha-3\ctg\alpha}{3\ctg^2\alpha-1} \end{aligned} $$
-
半角公式: $$ \begin{aligned} \sin\frac{\alpha}{2}&=\pm\sqrt{\frac{1- \cos\alpha}{2}}\ \cos\frac{\alpha}{2}&=\pm\sqrt{\frac{1+ \cos\alpha}{2}}\ \tg\frac{\alpha}{2}&=\pm\sqrt{\frac{1- \cos\alpha}{1+ \cos\alpha}}=\frac{\sin\alpha}{1+ \cos\alpha}=\frac{1- \cos\alpha}{\sin\alpha}\ \ctg\frac{\alpha}{2}&=\pm\sqrt{\frac{1+ \cos\alpha}{1- \cos\alpha}}=\frac{\sin\alpha}{1- \cos\alpha}=\frac{1+ \cos\alpha}{\sin\alpha} \end{aligned} $$
-
用半角的正切值表示三角函数: $$ \begin{aligned} \sin\alpha=\frac{2\tg\frac{\alpha}{2}}{1+\tg^2\frac{\alpha}{2}}\ \cos\alpha=\frac{1-\tg^2\frac{\alpha}{2}}{1+\tg^2\frac{\alpha}{2}}\ \tg\alpha=\frac{2\tg\frac{\alpha}{2}}{1-\tg^2\frac{\alpha}{2}}\ \ctg\alpha=\frac{1-\tg^2\frac{\alpha}{2}}{2\tg\frac{\alpha}{2}} \end{aligned} $$
-
三角函数和差化积公式: $$ \begin{aligned} \sin\alpha+\sin\beta&=2\sin\frac{\alpha+\beta}{2} \cos\frac{\alpha-\beta}{2}\ \sin\alpha-\sin\beta&=2\sin\frac{\alpha-\beta}{2} cos\frac{\alpha+\beta}{2}\ \cos\alpha+ \cos\beta&=2 \cos\frac{\alpha+\beta}{2} cos\frac{\alpha-\beta}{2}\ \cos\alpha- \cos\beta&=2\sin\frac{\alpha+\beta}{2}sin\frac{\beta-\alpha}{2} \end{aligned} $$
-
三角函数积化和差公式: $$ \begin{aligned} \sin{\alpha}\cos{\alpha}&=\frac{1}{2}\left[\sin{(\alpha+\beta)}+\sin{(\alpha-\beta)}\right]\ \cos{\alpha}\sin{\alpha}&=\frac{1}{2}\left[\sin{(\alpha+\beta)}-\sin{(\alpha-\beta)}\right]\ \cos{\alpha}\cos{\alpha}&=\frac{1}{2}\left[\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}\right]\ \sin{\alpha}\sin{\alpha}&=\frac{1}{2}\left[\cos{(\alpha+\beta)}-\cos{(\alpha-\beta)}\right] \end{aligned} $$
-
辅助角公式 $$ \begin{aligned} &\ a\cos{x}+b\sin{x}=c \ &\Rightarrow\frac{a}{\sqrt{a^2+b^2}}\cos{x}+\frac{b}{\sqrt{a^2+b^2}}\sin{x}=\frac{c}{\sqrt{a^2+b^2}} \ &\Rightarrow\cos{\phi}=\frac{a}{\sqrt{a^2+b^2}}\quad\sin{\phi}=\frac{b}{\sqrt{a^2+b^2}} \ &\Rightarrow\cos{\phi}\cos{x}+\sin{\phi}\sin{x}=\frac{c}{\sqrt{a^2+b^2}} \ &\Rightarrow\cos{x-\phi}=\frac{c}{\sqrt{a^2+b^2}}\quad\left(\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}\right) \ &\ x=\phi\pm\arccos{\frac{c}{\sqrt{a^2+b^2}}}+2k\pi\quad(\lvert c\rvert\le\sqrt{a^2+b^2}) \end{aligned} $$
第四节:三角函数和反三角函数
- 在 $[-\frac{\pi}{2},\frac{\pi}{2}]$ 上,函数 $y=sinx$,每一个值都取一次,所以在这个段上,这个函数是可逆的,即它有一个反三角函数。
- $x$ 的弧正弦是以弧度为单位计算的线段在 $[-\frac{\pi}{2},\frac{\pi}{2}]$ 的角度,其正弦等于 $x$。用 $\arcsin{x}$表示,即 $\sin(\arcsin{x})=x$ 或 $y=\arcsin{x}$,则 $x=siny,y\in[-\frac{\pi}{2},\frac{\pi}{2}]$
- 函数$y=\arcsin{x}$的基本性质
- 在定义域 $D(y)=[-1,1]$ 中,其函数是连续且单调递增的。
- 值域为 $E(y)=[-\frac{\pi}{2},\frac{\pi}{2}]$,即 $-\frac{\pi}{2}\le \arcsin{x}\le \frac{\pi}{2}$
- 函数为奇函数:$\arcsin{(-x)}=-\arcsin{x}$
- 由定义可知,$\sin(\arcsin{x})=x,-1\le x\le1$
- $\arcsin(\sin{x})=x,-\frac{\pi}{2}\le x\le \frac{\pi}{2}$
第五节:反三角函数及初步的三角方程
- 正弦
- $sinx=\alpha,x=(-1)^karcsin\alpha+k\pi,k\in {Z}$或 $$ x = \left{ \begin{aligned} &\arcsin\alpha+2\pi k,\ &\pi-\arcsin\alpha+2\pi k\quad k\in{Z} \end{aligned} \right. $$
- $\sin{x}=0,x=k\pi\quad k\in{Z}$$
- $\sin{x}=1,x=\frac{\pi}{2}+2k\pi\quad k\in{Z}$
- $\sin{x}=-1,x=-\frac{\pi}{2}+2k\pi\quad k\in{Z}$
- 余弦
- $\cos{x}=\alpha,x=\pm \arccos\alpha+2\pi k\quad k\in{Z}$
- $\cos{x}=0,x=\frac{\pi}{2}+k\pi\quad k\in{Z}$
- $\cos{x}=1,x=2k\pi\quad k\in{Z}$
- $\cos{x}=-1,x=(2k+1)\pi\quad k\in{Z}$
- 正切
- $\tg{x}=\alpha,(\cos{x}\neq0),x=\arctg\alpha+k\pi\quad k\in{Z}$
- $\tg{x}=1,x=\frac{\pi}{4}+k\pi\quad k\in{Z}$
- $\tg{x}=-1,x=-\frac{\pi}{4}+k\pi\quad k\in{Z}$
- 余切
- $\ctg{x}=\alpha,(\sin{x}\neq0),x=\arcctg\alpha+k\pi\quad k\in{Z}$
- $\ctg{x}=1,x=\frac{\pi}{4}+k\pi\quad k\in{Z}$
- $\ctg{x}=-1,x=\frac{3}{4}\pi+k\pi\quad k\in{Z}$
- 重要提示:在解三角函数方程时,应考虑和利用三角函数的性质,观察变换的等价性,考虑到方程中包含的所有函数的定义域。
第六节:解三角函数方程
- 基本思路
- 三角函数等价代换,减少不同名三角函数数量,转换为二次方程或多次方程求解。
- 常用代换:
- $\sin^{2}{\alpha}+\cos^{2}{\alpha}=1\quad\sin^{2}{\alpha}=1-\cos^{2}{\alpha}\quad\cos^{2}{\alpha}=1-\sin^{2}{\alpha};$
- $\cos{2\alpha}=\cos^2{\alpha}-\sin^2{\alpha}=2\cos^2{\alpha}-1=1-2\sin^2{\alpha}$
- $\tan{\alpha}=\frac{1}{\cot{\alpha}}$
- $a\sin{\alpha}+b\cos{\alpha}=0\quad\Rightarrow\quad a\tan{\alpha}+b=0$
- 和差化积、积化和差公式
百分数
- 百分数的意义:百分数是表示一个数是另一个数的百分之几的数,也叫百分率或百分比。百分数通常不写成分数的形式,而采用符号%(叫做百分号)来表示。百分数在工农业生产、科学技术、各种实验中有着十分广泛的应用,特别是在进行调查统计、分析比较时,经常要用到百分数。
- 两个问题:
- 简单百分比增长(простой процентный рост),即单利: $$S_n=S_0\cdot(1+\frac{pn}{100})$$
- 复杂百分比增长(сложный процентный рост),即复利: $$S_n=S_0\cdot(1+\frac{p}{100})^2$$
等差数列
- 等差数列是一种数字序列,其中的第一项等于$a_1$。从第二项开始,等于前一项加上一个常数$d$,这个常数又被称为公差
- 等差数列通项公式:
- $a_n=a_{n-1}+d,n=2,3,4...$
- 如果$d>0$,则这个数列是递增的;如果$d<0$,则这个数列是递减的;如果$d=0$,则这个数列是一个常数列
- 等差数列基本公式:
- $a_n=a_1+\left(n-1\right)d,n\in N$
- $S_n={na}_1+\frac{n\left(n-1\right)}{2}d=\frac{n\left(a_1+a_n\right)}{2},n\in N$
- $a_n=\frac{1}{2}\left(a_{n+1}+a_{n-1}\right),n\in N,n\geq 2$
- $a_k+a_{m-k+1}=a_1+a_m,k=1,2,...,m$
等比数列
- 等比数列是指从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列。这个常数叫做等比数列的公比,公比通常用字母$q$表示$(q\neq0)$,等比数列$b1\neq 0$。其中{$b_n$}中的每一项均不为0。注:$q=1$ 时,$b_n$为常数列。
- 等比数列公式
- $b_n=b_1q^{n-1},n\in{N}$
- $S_n=\frac{b_1\left(1-q^n\right)}{1-q}$
- $b_n=\sqrt{b_{n-1}\cdot b_{n+1}},n\in{N},n\ge{2}$
- 等比常数列($q=1$)
- $q=1, a_n=a_1$
- $S_n={na}_1$
最优解问题
- 要解决的问题类型
- 销量和售价(Оптимизация работы на производстве с учётом цен на рынке товара и факторов производства)
- 多部门生产(Многозаводское производство (включая разные заводы/ отели/ другие рабочие пространства))
- 运输问题(Транспортная задача)
- 解决方法
- 构建数据模型列方程式
- 求出方程定义域内的最值
导数
-
导数的定义
- 设函数 $y=f(x)$ 在点 $x_0$ 的某个领域内有意义,当自变量 $x$ 在 $x_0$ 处取得增量 $\Delta x$ (点 $x_0+\Delta x$ 仍在该领域内)时,相应的,因变量取得增量 $\Delta y=f(x_0+\Delta x)-f(x_0)$;如果 $\Delta y$ 与 $\Delta x$ 之比当 $\Delta x\rightarrow 0$ 时的极限存在,那么称函数 $y=f(x)$ 在点 $x_0$ 处可导,并称这个极限为函数 $y=f(x)$ 在点 $x_0$ 处的导数,记为 $f'(x_0)$ ,即 $$f'(x_0)=\underset{\Delta x\rightarrow 0}{\lim}\frac{\Delta y}{\Delta x}=\underset{\Delta x\rightarrow 0}{\lim}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$
-
常数和基本初等函数的导数 $$ \begin{aligned} C'&=0\ \(e^x)'&=e^x\ \(a^x)'&=a^x\ln{a}\ \(\log_ax)'&=\frac{1}{x\ln{a}}\ \(\ln{x})'&=\frac{1}{x}\ \(\sin{x})'&=\cos{x}\ \(\cos{x})'&=-\sin{x}\ \(\tan{x})'&=\frac{1}{\cos^2{x}}\ \(\cot{x})'&=-\frac{1}{\sin^2{x}}\ \end{aligned} $$
- 函数求导法则
- 令函数 $u=u(x)$ 与函数 $v=v(x)$ 在 $x$ 处可导,$C$为常数,$y=f[u(x)]$ 为变量 $x$ 的复合函数 $$ \begin{aligned} &(uv)'=u'v+v'u,(Cu)'=Cu'\ \&(u\pm v)'=u'\pm v'\ \&(\frac{u}{v})'=\frac{u'v-v'u}{v^2},(\frac{C}{v})'=-\frac{C}{v^2}\ \&y'_x=f'_u\cdot u'_x\ \end{aligned} $$
- 导数的几何意义
- 函数$y=f(x)$在点$x_0$处的导数$f'(x_0)$在几何上表示曲线$y=f(x)$在点$M_0(x_0,y_0)$处的切线的斜率,即 $f'(x)=\tan{\alpha}$ ,其中$\alpha$是切线的倾角,如下图。
- 根据导数的几何意义并应用直线的点斜式方程,可知曲线$y=f(x)$在点$M_0(x_0,y_0)$ 处的切线方程为
$$y-y_0=f'(x_0)(x-x_0)$$
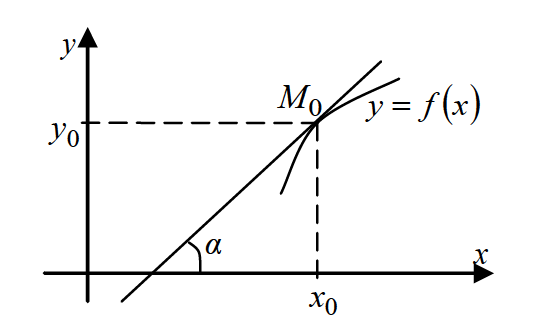
导数的应用
- 函数的增减性和极值点
- 如果函数 $f(x)$ 在 $x\in(a, b)$ 上单调递增,则任意两点 $a<x_1<x_2<b$,则 $f(x_1)<f(x_2)$。
- 如果 $f(x)$ 的导函数 $f'(x)>0 \quad \forall x \in (a, b)$,则 $f(x)$ 在 $x \in (a, b)$ 上单调递增。
- 如果 $f(x)$ 的导函数 $f'(x)<0 \quad \forall x \in (a, b)$,则 $f(x)$ 在 $x \in (a, b)$ 上单调递减。
- 如果对于某一区间上任意一点 $x \not = x_0$,$f(x)<f(x_0)$ 恒成立,则称 $x_0$ 为函数 $f(x)$ 的极值点(точка экстремума функции),$f(x_0)$ 写作 $max \ f(x)$
- $x_0$ 周围的区间必须连续
- $f'(x_0) = 0$ 是存在极值的必要不充分条件
- 给定区间 $(a, b)$,如果 $f(x) < 0 \quad x \in (a, x_0)$,$f(x) > 0 \quad x \in (x_0, b)$,那么 $x_0$ 为 $f(x)$ 在 $(a, b)$ 上的最小值
- 给定区间 $(a, b)$,如果 $f(x) > 0 \quad x \in (a, x_0)$,$f(x) < 0 \quad x \in (x_0, b)$,那么 $x_0$ 为 $f(x)$ 在 $(a, b)$ 上的最大值
- 给定区间 $(a, b)$,如果 $f(x) > 0 \quad x \in (a, x_0)$,$f(x) > 0 \quad x \in (x_0, b)$,或者 $f(x) < 0 \quad x \in (a, x_0)$,$f(x) < 0 \quad x \in (x_0, b)$,那么 $x_0$ 不是 $f(x)$ 的极值点
- 函数的最大最小值
- 函数 $f(x)$ 在区间 $[a, b]$ 上的最大值写作 $\underset{[a, b]}{\sup} f(x)$,最小值写作 $\underset{[a, b]}{\inf} f(x)$
- 在区间 $[a, b]$ 上的连续函数 $f(x)$ 总有最大值和最小值,需要把边界点进行比较。
- 在区间 $(a, b)$ 上可能没有最大值或最小值
立体几何
平面几何回顾
- 三角形中线的性质:
- 三角形的中线交于一点并以 $2:1$ 的比例将其划分(从顶部开始计算)
- 中位数将三角形分成两个等体积的三角形。
- 一个三角形的中线把它分成六个等体积的三角形。
- 令 $O$ 作为三角形 $ABC$ 的中线焦点,则 $S_{\bigtriangleup ABC}=3S_{\bigtriangleup AOB}=3S_{\bigtriangleup AOC}=3S_{\bigtriangleup BOC}$
- 在一个直角三角形中,中线延伸到斜边的长度等于它的一半。
- 推论:
- 直角三角形的外接圆圆心位于斜边中点上。
- 如果在一个三角形中,中线的长度等于它所对应的边长的一半,那么这个三角形就是直角三角形。
- 推论:
- 中线长:
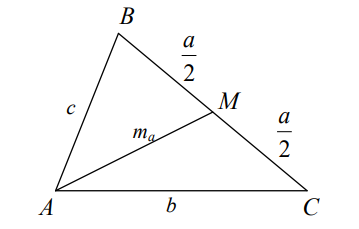
- 如果三角形 $ABC$ 的边长 $AB$、$AC$ 和 $BC$ 分别是 $c$、$b$ 和 $a$,延伸到 $BC$ 边的中线长度可以通过以下方式计算,根据公式 $m_{a}=\frac{1}{2}\sqrt{2b^{2}+2c^{2}-a^{2}}$
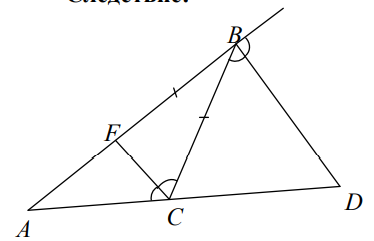
- 角平分线的性质:三角形的角平分线将三角形的平分线将对边分成与相邻边成比例的线段。
- 推论:如果 $BD$ 是三角形 $ABC$ 的外角的角平分线,则 $\frac{AD}{DC}=\frac{AB}{BC}$
- 四边形:
- 定义:四边形是由四点组成的图形,其中没有三点位于同一条直线上,四条线段依次连接这些点且不相交。
- 四边形的要素:
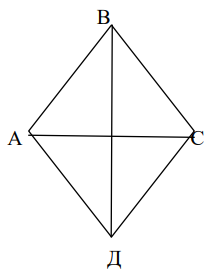
- $AB$、$BC$、$CД$ 和 $AД$ 是四边形的边。
- $A$、$B$、$C$、$Д$ 是四边形的顶点
- $АС$ 和 $ВД$ 是四边形的对角线
- 四边形的周长:$Р_{АВСД}=АВ+ВС+СД+АД$
- 四边形的边和角可以相邻的也可以是相对的。
- $AB$ 和 $AД$,$СД$ 和 $BC$ —— 邻边
- $AB$ 与 $СД$、$BC$ 与 $АД$ —— 对边
- $\angle A$ 和 $\angle B$ —— 邻角
- $\angle A$ 和 $\angle C$ —— 对角
- 定义:
- 连接四边形对顶点的线段被称为对角线。
- 四边形所有边的长度之和称为其周长。
- 如果四边形位于通过其相邻顶点的每条直线的一侧,则它是凸四边形。
- 与四边形的角相邻的角称为四边形的外角。
- 定理:四边形的内角之和为 $360º$:$∠A+∠B+∠C+∠D=360º$
- 平行四边形:
- 定义:
- 对边成对平行的四边形称为平行四边形。
- 平行四边形的高度是指从包含平行四边形边的直线上的任何一点到包含相反边的直线上的垂线。
- 性质:
- 对边和对角相等
- 对角线被交点平分
- 平行四边形的标志:
- 如果一个四边形的对边相等,那么这个四边形就是一个平行四边形。
- 如果四边形的两条对边相等且平行,那么这个四边形就是一个平行四边形。
- 如果一个四边形的对角线被交点平分,那么这个四边形就是一个平行四边形。
- 定义:
- 矩形:
- 定义:所有角都为直角的平行四边形。
- 性质:
- 矩形的对角线是相等的。
- 标志:
- 如果一个平行四边形的一个角是直角,那么这个平行四边形就是一个矩形。
- 如果一个平行四边形的对角线相等,那么它就是一个长方形
- 菱形
- 定义:菱形是所有边都相等的平行四边形。
- 性质:
- 平行四边形的所有性质。
- 菱形的对角线是垂直的,是它的角的平分线。
- 标志:
- 如果平行四边形的对角线垂直,则是菱形。
- 如果平行四边形的对角线是其角的平分线,则是菱形。
- 正方形:
- 定义:正方形是所有边都相等的矩形,或者是所有角都相等的菱形。
- 性质:
- 正方形的四角都是直的。
- 正方形的对角线相等。
- 正方形的对角线是垂直的并且是它的角的平分线。
- 梯形:
- 定义:如果 $BC$ 和 $AD$ 平行,四边形 $ABCD$ 称为梯形。
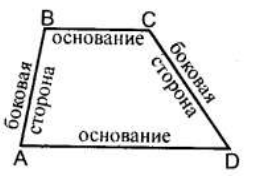
- $AB$ 和 $CD$ - 侧边
- $BC$ 和 $AD$ - 底边
- 类别:
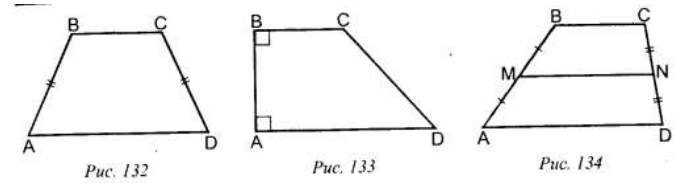
- 图132:等腰梯形
- 图133:直角梯形
- 图134:$M$ 是 $AB$ 的中线,$N$ 是 $CD$ 的中线,$MN$ 是梯形的中线。
- 等腰梯形的性质:
- 在一个等腰梯形中,每个底角的角度是相等的。
- 在一个等腰梯形中,对角线是相等的。
- 等腰梯形的标志:
- 如果梯形底边的角相等,则它是等腰的。
- 如果梯形的对角线相等,那么它是等腰的。
- 定义:如果 $BC$ 和 $AD$ 平行,四边形 $ABCD$ 称为梯形。
- 四边形
- 性质:任意四边形边的相邻边的中点两两相连可以构成平行四边形
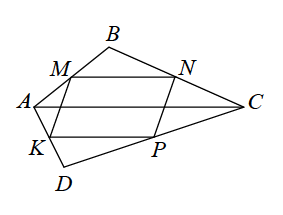
- 推论:
- 如果ABCD是凸四边形,$M$、$N$、$P$、$K$分别是其边$AB$、$BC$、$CD$ 和 $AD$ 的中点,则$S_{MNPK} = \frac{1}{2} S_{ABCD}$
- 矩形的相邻边的中点两两相连可以构成菱形
- 等腰梯形相邻边的中点两两相连可以构成菱形
- 菱形相邻边的中点两两相连可以构成矩形
向量
- 向量表示法
- $\vec{a}$
- $\vec{AB}$
- 向量的长度
- $\lvert \vec{a} \rvert$
- $\lvert \vec{AB} \rvert$
- 向量平行($\vec{a} \parallel \vec{b}$)
- 两个向量平行或重合
- 向量相等($\vec{a} = \vec{b}$)
- $\lvert \vec{a} \rvert = \lvert \vec{b} \rvert$
- 两个向量平行且同向
- 向量的平行四边形法则
- $\vec{c} = \vec{a} + \vec{b}$
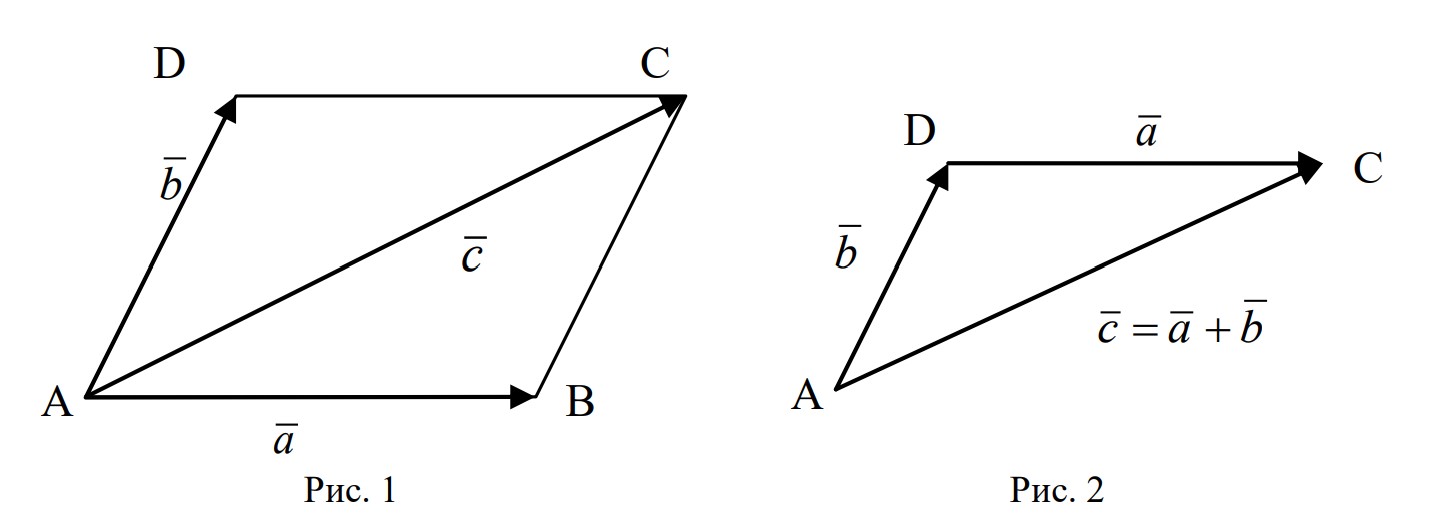
- $\vec{c} = \vec{a} + \vec{b}$
- 向量的乘法($\alpha\vec{a} = \vec{c}$)
- $\lvert \vec{c} \rvert = \lvert \alpha \vec{a} \rvert = \lvert \alpha \rvert \lvert \vec{a} \rvert$
- 两向量平行,根据 $a$ 的正负判断向量的方向关系
- $\vec{a} \parallel \vec{b} \Leftrightarrow \alpha\vec{a} = \vec{b} \quad (\vec{b} \ne \vec{0})$
-
三维向量
- 设有点 $M(x_1, y_1, z_1)$,点 $N(x_2, y_2, z_2)$
- 以原点 $O$ 为起始点,得到向量:$\vec{m} = \vec{OM} = {x_1, y_1, z_1}$ 和 $\vec{n} = \vec{ON} = {x_2, y_2, z_2}$
- 根据向量减法,得到向量 $\vec{MN} = \vec{n} - \vec{m} = {x_2-x_1, y_2-y_1, z_2-z_1} $,向量 $\vec{MN}$ 即为点 $M$到和点 $N$ 组成的向量
- 根据向量模的计算,得到 $\lvert \vec{MN} \rvert = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}$
-
如果线端 $MN$ 上有一点 $C$,使得 $\frac{MC}{CN} = \lambda$
- 则向量 $\vec{OC} = \vec{c}$ 可求
$$ \vec{OC} = \frac{\vec{r_A}+\lambda\vec{r_B}}{1+\lambda}\Leftrightarrow \left{\begin{aligned} x_C &= \frac{x_A+\lambda x_B}{1+\lambda}\ y_C &= \frac{y_A+\lambda y_B}{1+\lambda}\ z_C &= \frac{z_A+\lambda z_B}{1+\lambda}\ \end{aligned}\right. $$
- $\lambda = 1$ 时有点 $C$ 平分线端 $AB$,则有
$$ \vec{OC} = \frac{\vec{r_A}+\vec{r_B}}{2}\Leftrightarrow \left{\begin{aligned} x_C &= \frac{x_A+x_B}{2}\ y_C &= \frac{y_A+y_B}{2}\ z_C &= \frac{z_A+z_B}{2}\ \end{aligned}\right. $$ - 向量坐标 - 笛卡尔坐标系中向量的坐标是该向量在坐标轴上的投影 - 有 $\vec{a}$、$\vec{b}$ 两向量:
$$\begin{aligned} \vec{a} &= {a_x, a_y, a_z}\ \vec{b} &= {b_x, b_y, b_z}\ \end{aligned}$$
- 若 $\vec{a} = \vec{b}$,则 $a_x=b_x, a_y=b_y, a_z=b_z$
- $\lvert \vec{a} \rvert = \sqrt{a_x^2 + a_y^2 + a_z^2}$
- $\vec{a} \plusmn \vec{b} = {a_x\plusmn b_x, a_y\plusmn b_y, a_z\plusmn b_z}$
- $\alpha\vec{a} = {\alpha a_x, \alpha a_y, \alpha a_z}$
- 若向量 $\vec{a}$、$\vec{b}$ 共线,则 $\vec{a} \parallel \vec{b}$,则有 $\frac{a_x}{b_x}=\frac{a_y}{b_y}=\frac{a_z}{b_z}$
- 三维向量的内积(点乘)(Скалярное произведение)
- 对任意两向量有 $$\vec{a}\cdot\vec{b} = \lvert \vec{a} \rvert \cdot \lvert \vec{b} \rvert \cdot \cos{(\vec{a}, \vec{b})}$$
- 若有 $\vec{a} = {a_x, a_y, a_z}$ 且 $\vec{b} = {b_x, b_y, b_z}$,则有 $$\vec{a}\cdot\vec{b}=a_xb_x+a_yb_y+a_zb_z$$
- $\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}$
- $\vec{a}\cdot\vec{a} = \lvert \vec{a} \rvert^2$ 或有 $\vec{a}^2 = \lvert \vec{a} \rvert^2$,因此可得 $\lvert \vec{a} \rvert = \sqrt{\vec{a}^2}$
- 若 $\vec{a} \perp \vec{b}$,则有一般式 $\vec{a}\cdot\vec{b} = 0$ 或坐标式 $a_xb_x + a_yb_y + a_zb_z = 0$
- 两向量之间的夹角
$$ \cos{(\vec{a}, \vec{b})} = \frac{\vec{a}\cdot\vec{b}}{\lvert \vec{a} \rvert \cdot \lvert \vec{b} \rvert} = \frac{a_xb_x + a_yb_y + a_zb_z}{\sqrt{a_x^2+a_y^2+a_z^2}\sqrt{b_x^2+b_y^2+b_z^2}} $$ - 任意维数向量的内积(点乘) - 设有两向量
$$\begin{aligned} a &= (a_1, a_2, ..., a_n)\ b &= (b_1, b_2, ..., b_n)\ \end{aligned}$$
- 向量 $\vec{a}$ 和 $\vec{b}$ 的内积公式
$$a \cdot b = a_1b_1 + a_2b_2 + ... + a_nb_n$$
- 内积的几何意义
- 点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在 b 向量在 a 向量方向上的投影。
-
任意维数向量的外积(叉乘)
- 两个向量的外积,又叫向量积、叉乘等。外积的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
- 设有两向量
$$\begin{aligned} a &= (x_1, y_1, z_1)\ b &= (x_2, y_2, z_2)\ \end{aligned}$$
- 向量的外积公式(其中 $\vec{i}=(1,0,0)\ \vec{j}=(0,1,0)\ \vec{k}=(0,0,1)$)
$$\begin{aligned} a \times b &= \begin{vmatrix} i & j & k \ x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 \end{vmatrix}\ &= (y_1z_2-y_2z_1)\vec{i} - (x_1z_2-x_2z_1)\vec{j} + (x_1y_2-x_2y_1)\vec{k} \end{aligned}$$
- 根据 $\vec{i}=(1,0,0)\ \vec{j}=(0,1,0)\ \vec{k}=(0,0,1)$ 可得新的叉乘计算公式:
$$ a \times b = (y_1z_2-y_2z_1, - (x_1z_2-x_2z_1), x_1y_2-x_2y_1) $$
- 叉乘几何意义
- 在三维几何中,向量 a 和向量 b 的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于 a 和 b 向量构成的平面。
内切圆和外接圆
- 内切圆:与多边形各边都相切的圆叫做多边形的内切圆。特殊地,与三角形三边都相切的圆叫做三角形的内切圆,圆心叫做三角形的内心,三角形叫做圆的外切三角形。三角形的内心是三角形三条角平分线的交点。三角形一定有内切圆,其他的图形不一定有内切圆,且内切圆圆心定在三角形内部。任何一个正多边形都有内切圆,内切圆的圆心就是正多边形的中心,内切圆一定与正多边形每条边的中点相接触。
- 外接圆:与多边形各顶点都相交的圆叫做多边形的外接圆。三角形有外接圆,其他的图形不一定有外接圆。 三角形的外接圆圆心是任意两边的垂直平分线的交点。 三角形外接圆圆心叫外心。如果四边形的对角和为$180°$,则该四边形有外接圆,反之亦然。
平面
-
空间中的平面方程:
$$Ax+By+Cz+D=0$$
- $D=0$,则平面穿过原点
- 如果 $A = 0$($B = 0$ 或 $C = 0$),则该平面平行于 $Ox$ 轴(分别为 $Oy$ 轴或 $Oz$ 轴)。
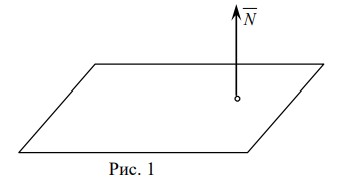
- 垂直于平面的法向量 $\vec{N} = {A, B, C}$
-
通过某点坐标 $M(x_0, y_0, z_0)$ 和法向量 $\vec{N} = {A, B, C}$ 可得平面方程:
$$A(x-x_0) + B(y-y_0) + C(z-z_0) = 0$$
-
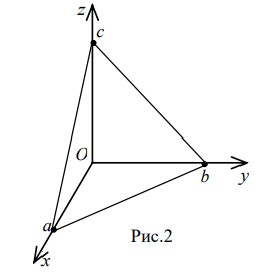
通过与坐标轴截距 $A(a,0,0)\ B(0,b,0)\ C(0,0,c)$ 可得平面方程:
$$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$$
-
过任意不重合三点 $M_1(x_1, y_1, z_1)\ M_2(x_2, y_2, z_2)\ M_3(x_3, y_3, z_3)$ 的平面方程:
$$ \begin{aligned} Ax_1 + By_1 + Cz_1 + D = 0\ Ax_2 + By_2 + Cz_2 + D = 0\ Ax_3 + By_3 + Cz_3 + D = 0\ \end{aligned} $$
-
任意一点 $M(x_0, y_0, z_0)$ 到平面 $Ax+By+Cz+D=0$ 的距离
$$d=\frac{\lvert Ax_0+By_0+Cz_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$$
-
通过两个平面的法向量 $\vec{N_1}={A_1,B_1,C_1}\ \vec{N_2}={A_2,B_2,C_2}$ 计算平面的夹角(二面角)
$$\cos{\varphi} = \lvert\cos{\varphi}\rvert=\frac{\lvert\vec{N_1}\cdot\vec{N_2}\rvert}{\lvert\vec{N_1}\rvert\lvert\vec{N_2}\rvert}$$
-
平行平面间的系数关系
$$\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}$$
-
垂直平面间的系数关系
$$A_1A_2+B_1B_2+C_1C_2=0$$
直线
-
空间中的直线被表示为两个平面的交线:
$$ \begin{aligned} A_1x + B_1y + C_1z + D_1 = 0\ A_2x + B_2y + C_2z + D_2 = 0\ \end{aligned} $$
-
设向量 $\vec{S}={m,n,p}$ 与已知直线平行,且已知直线过点 $M(x_0,y_0,z_0)$,则有以下结论
$$ \begin{aligned} &\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}=t\ &\left{ \begin{aligned} x&=mt+x_0\ y&=nt+y_0\ z&=pt+z_0\ \end{aligned} \right. \end{aligned}$$
-
已知直线穿过两点 $M_1(x_1,y_1,z_1)$ 和 $M_2(x_2,y_2,z_2)$,可得直线方程
$$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$$
-
已知直线穿过两点 $M_1(x_1,y_1,z_1)$ 和 $M_2(x_2,y_2,z_2)$,可得关系式
$$\begin{aligned} \frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1}\ \frac{x-x_2}{m_2}=\frac{y-y_2}{n_2}=\frac{z-z_2}{p_2}\ \end{aligned}$$
-
某项分母为 0 说明垂直于某轴
-
因此可得与两直线平行的向量
$$\begin{aligned} \vec{S_1}={m_1,n_1,p_1}\ \vec{S_2}={m_2,n_2,p_2} \end{aligned}$$
- 可得两直线夹角
$$\cos{\varphi} = \frac{\vec{S_1}\cdot\vec{S_2}}{\lvert\vec{S_1}\rvert\lvert\vec{S_2}\rvert}$$
- 两直线平行的条件
$$\frac{m_1}{m_2}=\frac{n_1}{n_2}=\frac{p_1}{p_2}$$
- 两直线垂直的条件
$$m_1m_2+n_1n_2+p_1p_2=0$$
-
参考文献:
- 预科数学课件